Die Newton-Widerlegung
Und nun folgt eine kurze Widerlegung der Gravitationstheorie des größten Physikers aller Zeiten: Isaac Newton.
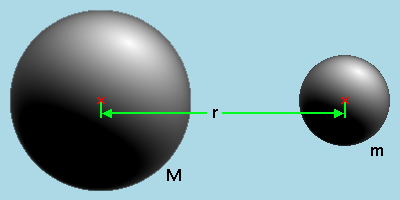
Nach der Gravitationstheorie von Isaac Newton läßt sich die Masse eines Körpers in dessen Schwerpunkt vereinigt denken. Die Anziehungskraft auf beide Kugeln im obigen Bild ist dann:
F = g*M*m/r²
Dabei meint M die Masse des einen Körpers, m die des anderen, r ist der Abstand der beiden Schwerpunkte der beiden Körper und g ist "die Gravitationskonstante" mit der komischen Einheit: N*m²/kg². Komisch deshalb, weil man sich nichts unter Masse zum Quadrat vorstellen kann. Die "Gravitationskonstante" soll im ganzen Universum überall gleich sein.
Die Körper müssen aber keine Kugeln sein, es gehen auch Ringe:
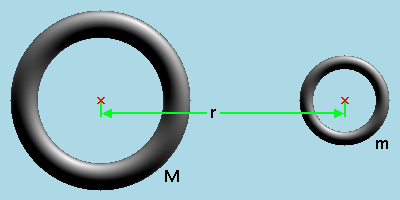
Hier bleibt alles beim alten.
F = g*M*m/r²
Man kann den Abstand r natürlich variieren.
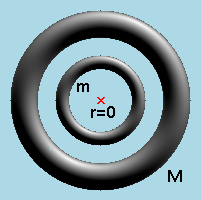
Ooops! Was ist da passiert? Der Abstand der beiden Schwerpunkte der beiden Ringe ist ja null. Und Dividieren durch null geht nicht! Die Kraft wäre ja unendlich. Dem ist aber nicht so.
Fazit: Newton ist damit widerlegt.
Ist auch logisch irgendwie. Eine Kraft die nur anziehend wirkt, würde ja das ganze Universum verklumpen. Und thermische Neutronen fallen auch nicht herunter. Und das Planetensystem wäre nie stabil: eine kleine Veränderung der Umlaufgeschwindigkeit eines Körpers würde ihn sofort aus dem Sonnensystem hinaus katapultieren oder in die Sonne stürzen lassen. Von der Unmöglichkeit der Lösung des Dreikörperproblems wusste schon Poincaré ein Lied zu singen.
Und jedes Atom des Universums müsste zu jeder Zeit wissen, wo alle anderen Atome des Universums sind. Der Computer, den so ein Atom haben müsste, wäre größer als das Universum selbst.
Saturn und Jupiter sind kugelrund. Nach Newton ist ihre Masse noch kleiner als die von Luft, weswegen sie Gasplaneten genannt werden. Aber: bestünden sie aus Gas, dann wären sie ein Nebel und also wolkig wie so ein Crab-, Orion-Nebel oder so aber nicht kugelrund! Dann strahlen beide mehr Energie ab, als sie von der Sonne bekommen. Wo soll denn ein Gas die Energie hernehmen? Auf der Sonnenoberfläche brodelt es. Und dann sind Saturn und Jupiter bunt. Ein Gas müsste sich längst durchmischt haben. Wo also sollen die Farben herkommen?
Dann haben Saturn, Jupiter und Uranus Ringe exakt über dem Äquator. Nach Newton ist der Äquator eines Planeten jedoch nicht besonders ausgezeichnet.
Um das Verklumpen des Universums nach Newton zu erklären, brauchen dann monotheistisch gepolte Physiker den Urknall: das Universum verklumpt zwar, aber noch nicht sofort, erst muss die Bewegungsenergie des Urknalls aufgebraucht sein. Das finden die dann konform mit ihrem Buch.
(Für Leute, die meinen, Newton gelte nur in einem "Außerhalb", innerhalb der Ringe würde sich die Gravitationskraft aufheben, deswegen würde dort gelten: 0/0 = 0, kann ich sagen: Apfelringe schweben nicht. Ich kann den inneren Ring auch um 90° aus der Tischebene herausdrehen, dann ist er außen. Man kann statt Apfelringen natürlich auch Bananen nehmen...)
Hebelgesetz
Eine Balkenwaage in einem homogenen Isobarenfeld befindet sich im Gleichgewicht, wenn sie genau im gemeinsamen Schwerpunkt der zu vergleichenden Massen gehalten wird.
Balkenwaage

zwei Massen; nah beeinander

zwei Massen; entfernt
Und da gilt das Hebel-Paradox: je weiter entfernt die kleine Masse ist, umso schwerer wiegt sie, denn im Hebelgesetz geht sie linear mit der Entfernung. Das bedeutet: Integration über ein Erdatom, das sich in die Andromeda-Galaxie verirrt hat, katapultiert den gemeinsamen Schwerpunkt Erde plus eben dieses Atom aus dem Sonnensystem, einfach weil die Andromeda-Galaxie so weit weg ist.
Und da kann Newton nicht einfach sagen: Och, die Andromeda-Galaxie ist so weit weg, darüber integriere ich nicht bei meiner Schwerpunktbestimmung sondern nur bis zu einer gewissen, grün gestrichelten Linie, alles was dahinter ist, interessiert mich nicht. Ich interessiere mich nur für sichtbare Festkörper und Flüssigkeiten und nicht für interstellare Gase.
Nein, diese Grenzziehung ist willkürlich und damit unzulässig.
"Wir bauen uns einen Baumarkt."
"Chef, wir haben keinen Beton."
"Dann geht in den Baumarkt, welchen holen."
Newton: Finale Erledigung
1.) Schwerpunktbestimmung Halbkugel
Das Volumen einer nichtnegativen, stetigen Funktion f(x), die um die x-Achse rotiert, ist:
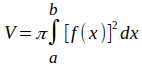
Für einen Kreis gilt:
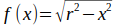
Bei einer Halbkugel geht x von 0 bis r. Wegen der Rotationssymmetrie muss der Schwerpunkt auf der x-Achse liegen. Im Schwerpunkt x = s muss das Integral von 0 bis s gleich dem Integral von s bis r sein.
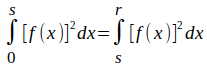
Eingesetzt ergibt das:
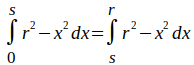
Integration liefert:
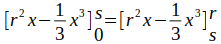
Daraus folgt die kubische Gleichung:
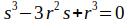
Diese hat drei Lösungen, die Lösung, die im Intervall 0 bis r liegt, ist:
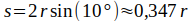
Zerteilt man nun gedanklich eine Kugel in zwei Halbkugeln in der y-z-Ebene, dann liegen die beiden Schwerpunkte S1 und S2 bei [-s, 0, 0] und [s, 0, 0].
2.) Gedankenexperiment
Wir schauen uns nun eine Kugel an, die in zwei Halbkugeln geteilt wurde, wobei die beiden Halbkugeln mit ihren Schwerpunkten aneinander bleiben und so zusammen die ursprüngliche Kugel bilden. Der Schnitt ist also nur virtuell.
Zerteilte Kugel
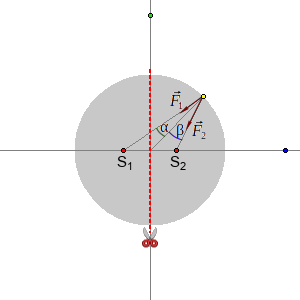
Der Schnitt verläuft gedanklich in der y-z-Ebenen.
Der blaue Punkt liegt auf der x-Achse.
Der blaue Punkt liegt auf der x-Achse.
Schaut man sich nun den gelben Punkt an, dann stellt man fest, dass α kleiner als β und F1 kleiner als F2 ist, da S1 weiter von dem Punkt weg ist als S2. Damit zeigt die Gesamtkraft F1+F2, die auf den gelben Punkt wirkt, nicht zum Kugelmittelpunkt sondern etwas mehr in Richtung von S2. Die Richtung der Gravitationskraft zweier Halbkugeln kann aber nicht davon abhängen, wie man sich einen Schnitt denkt.
Für den grünen Punkt ergibt sich, dass die Gravitationkraft nach Newton weniger geworden ist, weil S1 und S2 weiter weg von ihm sind als der Kugel-Mittelpunkt. Auf den blauen Punkt hingegen wirkt nach Newton eine größere Kraft, weil die Gravitationskraft nach Newton nicht linear mit dem Abstand geht, gleicht der Verlust durch die höhere Entfernung von S1 nicht den Dazugewinn durch die Annäherung von S2 aus.
Eine Gravitationskraft einer Kugel darf aber nicht davon abhängen, wie man sich einen Schnitt durch die Kugel denkt. D.h. man darf sich die Masse einer Halbkugel zur Ermittlung eines Gravitationspotentials nach Newton nicht im Schwerpunkt vereinigt denken. Damit ist Newton auch außerhalb von Kugeln widerlegt. q.e.d.
Wie Newton auf sein "Gravitationsgesetz" kam
Galilei hatte herausgefunden, dass ein in Luft geworfener Stein eine Parabelbahn beschreibt. Er konnte zeigen, dass sich diese Parabelbahn aus der Überlagerung zweier Bewegungen zusammensetzt.
Wurfparabel
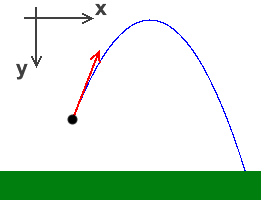
Längs zur Erdoberfläche (in x-Richtung) bewegt sich der Stein in Luft mit gleichmäßiger Geschwindigkeit und in Richtung senkrecht der Erdoberfläche macht der Stein eine gleichmäßig beschleunigte Bewegung. Die Wurfrichtung ist eine Tangente an der Wurfparabel.
Nun war von den Mathematikern gefordert, eine Theorie zu finden, die zu einer Kurve die Tangente an jedem Kurvenpunkt berechnet. Diese Aufgabe lösten zuerst Newton und etwas später Leibniz. Letzterer ohne Kenntnis des Ergebnisses von Newton, da Newton als Alchimist sein Wissen lange Jahre geheim hielt.
Nachdem Columbus nach den Wikingern erneut bewies, dass die Erde eine Kugelgestalt hat und Kopernikus die Sonne in den Mittelpunkt des Planetensystems stellte, hatten die mosaischen Monotheisten mit ihrem Büchlein ein Problem. Der damalige katholische Pontifex Maximus als Nachfolger des weisen Augustus in Rom beauftragte daher über Kaiser Rudolf II den Protestanten Kepler, die Theorie des Kopernikus zu widerlegen. Kepler bastelte erst an einem Planetenmodell, das er in die Platonischen Körper setzte. Nachdem er erkennen musste, dass das Unsinn ist, verwarf er diese Idee und fand heraus, dass wenn man für die Planetenbahnen Ellipsen annimmt mit der Sonne in einem der Brennpunkte der Ellipse, dann liefert das Kopernikanische Weltbild endlich genauere Himmelsdaten als das Ptolemäische. Damit war dann das Geozentrische Weltbild erledigt.
Und nun hatten die Geistesgrößen nach Kepler eine knifflige Nuss zu knacken. Gefragt war es, eine Theorie zu finden, die im Ergebnis eine Kepler-Ellipse liefert. Newton gelang dies, indem er eine Zentralkraft postulierte, die mit 1/r² geht. Dazu musste er dann nach der Differentialrechnung erst die umgekehrte Integralrechnung erfinden, denn er brauchte für seine Zentralkraft ein Gravitationszentrum. Er musste dazu zeigen, dass wenn man die Masse der Erde in unendlich kleine Pakete teilt und diese aufsummiert, dass sich dann die Stärke des Gravitationszentrums ergibt.
Es ist ein Zirkel- (bzw. Ellipsen- ;-)) schluss, wenn man erst aus den Kepler-Ellipsen die Gravitationskraft beweist und dann anschließend aus einem Gravitationsfeld die Ellipsen-Gestalt der Planetenbahnen beweist.
Die meisten Physikstudenten erkennen diesen Zirkelschluss allerdings nicht, weil sie mit dem Lernen der Mathematik (Verallgemeinertes 1/r**n Potential mit Reibung...) genug beschäftigt sind.
Leibniz widersprach Newtons Gravitationgesetz heftig. Er warf Newton vor, mit einer nur anziehend wirkenden Kraft dem Okkulten die Tür in die Wissenschaft geöffnet zu haben. Was sollte das sein, eine Fernwirkungs-Kraft, die durch ein Vakuum wirkt und auch noch ohne Zeitverlust?
Historisches:
Als Entdecker der Infinitesimalrechnung können weder Newton noch Leibniz gelten, denn vor ihnen zeigte Kepler 1615 in seiner Nova steriometria den Weg bei seiner Berechnung des Inhalts eines Weinfasses auf. Er dachte sich das Volumen einer Kugel durch lauter Kegel mit der Höhe des Radius zusammengesetzt vor, die sich in der Kugelmitte treffen und kam so auf das Volumen einer Kugel von 1/3*Oberfläche*Radius.
Vor Kepler hatten bereits in der Antike Euklid und Archimedes das Rechnen mit unendlich kleinen Teilen gezeigt mit ihren Exhaustionsmethoden. Euklid in seinem X. Buch und Archimedes fand bei der Bestimmung der Parabelfläche durch die Reihe 1/4 + (1/4)**2 + (1/4)**3 + ... + (1/4)**n = 1/3 den Wert beliebig nah erreicht.
Übrigens: die antiken Griechen wie Platon wollten die Natur auf perfekte Objekte zurückführen. Und perfekt waren für sie Kugeln und Kreise. Und so benutzte Ptolemäus Kreise (Deferent und Epizykel), um sein Weltbild zu erklären, bis Kepler sagte: es sind Ellipsen! Aber was sind Ellipsen? Ein in einem Kreis abrollender Kreis! Also auch wieder Kreise. Der Deferent hat also lediglich seine Mitte verloren. Eine Theorie muss einfach sein und einfacher als Kreise geht nicht. Die Lösung der Planetenbewegung wird wohl in der Lösung der Hillschen Differentialgleichung liegen.
