Die Lemniskaten

Die Bezeichnung Lemniskate leitet sich aus dem Lateinischen ab und bedeutet: Kettenglied. Ein Schmied, der eine Kette schmiedet, schlägt die runden Kettenglieder oval und verdrillt sie noch ein bisschen, damit die Kette länger wird und besser über Hindernisse läuft.
Als liegende Acht hat sie auch die Bedeutung der Unendlichkeit, da sie keinen Anfang und kein Ende hat, in der Mitte aber trotzdem etwas passiert.
Alle Neune!
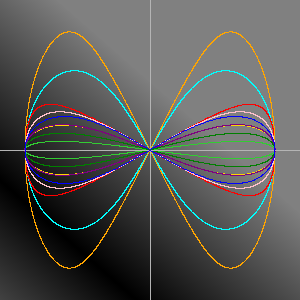
mit gleichem Polarwinkel
Für meine Windmühlen suchte ich einen Weg, wie ich aus einer Kreisbewegung eine (sphärische) Lemniskate zaubern konnte. Die ebenen drei bekannten Lemniskaten
- die Lemniskate von Bernoulli
- die Lemniskate von Booth
- die Lemniskate von Gerono
taugten nicht für meine Anforderungen. Ich fand zuerst die Kardan-Lemniskate. Eigentlich hätte die schon gereicht, aber die Mathematik dahinter ließ mich einfach nicht los. Und so fand ich als nächstes die Basislemniskate. Anschließend fand ich noch die Doppel-Lemniskate und danach habe ich die neuen Lemniskaten der Einfachheit halber durchnumeriert. Mittlerweile sind es abzählbar neun.
Nun kann ich auch den Öffnungwinkel der Kardan-Lemniskate fließend von 0° bis θ variieren.
Mathematisch kann man als Lemniskate definieren:
Eine Lemniskate ist die geschlossene Bahn eines Punktes in einer 2-dimensionalen Riemannschen Mannigfaltigkeit, deren sich stetig veränderende intrinsische Krümmung 4 Symmetrie-Phasen durchläuft. Am Ende der ersten Viertel-Phase wird die Krümmung null ohne einen Vorzeichenwechsel vorher, im zweiten Viertel ist sie punktsymmetrisch zur Stelle, wo sie null war. Die letzten beiden Viertel sind dann achsensymmetrisch gespiegelt zu den ersten beiden Vierteln. (Wie so eine Cosinus-Funktion halt.)
Mathematisch ausgedrückt:
Sei f: [0, T] → ℝ³ eine Kurve und liege auf der Fläche g: (u, v) → ℝ³ und K(t) ≥ 0, für t ∈ [0, T/4[ und K(T/4) = 0, dann gilt für die intrinsische Krümmung k i der Kurve:
k i(t) = {K(t), für t ∈ [0, T/4[,
-K(T/2-t), für t ∈ [T/4, T/2[,
-K(t-T/2), für t ∈ [T/2, 3*T/4[,
K(T-t), für t ∈ [3*T/4, T]}
und f(0) = f(T)
Diese Definition hat den Vorteil, dass man sie auch auf gekrümmten Flächen wie Tori, Paraboloiden etc. anwenden kann. Welche Eigenschaft die Fläche haben muss, dass man nach den 4 Phasen wieder am Ursprungsort ankommt? Ähm, das muss man noch klären...
(Die intrinsische Krümmung k i ist die Krümmung einer Kurve in der Fläche. Bei einem Radfahrer ist die Krümmung der Bahn die Lenkerstellung (geteilt durch den Achsabstand, wobei das Fahrrad unendlich klein aber nie null ist...). Fährt er auf dem Äquatorkreis einer Kugel, ist das Lenkrad gerade, damit ist die intrinsische Krümmung k i = 0. Fährt er den gleichen Kreis auf der Halbkugel-Ebenen ab, dann ist die intrinsische Krümmung in der Fläche der Ebenen k i = 1 / r.
Um die intrinsische Krümmung der Kurve auf einer Fläche zu berechnen, muss man an die Kurvenpunkte die Schmiegebene der dortigen Fläche anlegen, die von dem Tangentenvektor und dem Hauptnormalenvektor der Kurve aufgespannt wird. In dieser Schmiegebenen erhält man die gesuchte Krümmung durch die Anwendung des Satzes von Meusnier.)
Im Unterschied zu den Lemniskaten von Bernoulli, Booth und Gerono auf der Ebenen brauche ich Lemniskaten auf der gekrümmten Oberfläche einer Kugel für meine Windmühlen und dazu muss die Definition der Lemniskate etwas allgemeiner sein und die drei erst genannten Lemniskaten als Sonderfall beinhalten.
Analog dazu kann ich drei Definitionen des Kreises anbieten:
Ein Kreis ist
- die Menge aller Punkte, die zu einem Flächenpunkt den gleichen Abstand haben (Punktdefinition)
- die Bahn eines Punktes, die überall die gleiche intrinsische Krümmung hat (Liniendefinition)
- die Bahn eines Punktes mit vorgegebener Länge, die die Fläche in zwei Teilflächen teilt, wobei der Quotient aus kleinerer Fläche durch größere Fläche maximal ist. (Flächendefinition)
In der Ebenen oder auf einer Kugel sind alle drei Definitionen äquivalent.
Auf einem Paraboloid z.B. gibt es also drei verschiedene Typen von Kreisen bei euklidischer Abstands- und Flächennorm. (Euklidische Abstandsnorm: dr² = dx² + dy², euklidische Flächennorm: dA = dx * dy; mit dx ⊥ dy. Faktisch interessiert nur die euklidische Norm, da man nur sie in Materie basteln kann.) Auf einer gekrümmten Fläche mit nicht überall gleicher Krümmung (= Kugel) ist der Kreis also orts- und definitionsabhängig! Auch logisch irgendwie. Die Punktdefinition ist am Logischsten, da man mit einem Kreis immer auch einen Radius assoziiert. Der Radius hier folgt den Geodäten, die vom Mittelpunkt ausgehen. Definition 1 und 2 sind mathematisch nicht äquivalent, denn eine geschlossene Spiralbahn auf einem Torus um dessen Mitte läßt sich prinzipiell nicht platt bügeln wie z.B. ein Paraboloid.
Torus-Spirale

Symbolbild (eine Kurve auf einer Torus-Fläche mit konstanter intrinsischer Krümmung zu beschreiben, die nach n Umläufen wieder zu ihrem Startpunkt mit gleicher Startrichtung kommt, ist nicht so trivial, ähm, wohl unmöglich)
die rote Wendel ist nach Definition 1 kein, nach Definition 2 ein Kreis
die rote Wendel ist nach Definition 1 kein, nach Definition 2 ein Kreis
Anmerkung: Die Bezeichnung "geodätische Krümmung" gefällt nicht, denn eine Geodäte ist nach Definition die lokal kürzeste Verbindung zweier Punkte auf einer Fläche und die hat innerhalb der Fläche immer die Krümmung 0. Der Begriff ist damit ein Widerspruch in sich. "Intrinsische Krümmung" beschreibt die Sache besser.
Doppelkegel
Der blaue "Kreis" hat den gleichen Abstand vom gelben Punkt wie der rote.
Er ist deswegen nach Kreisdefinition 1 nur ein Halbkreis!
Er ist deswegen nach Kreisdefinition 1 nur ein Halbkreis!
Lemniskaten-Definition über die Polardarstellung
Weil man die Bahn eines Punktes auf einer gekrümmten Fläche bei vorgegebener intrinsischer Krümmung nur sehr schwer bis unmöglich bestimmen kann, ist eine Definition der allgemeinen Lemniskate über die Polarkoordinaten zweckmäßiger.
Rotierende geodätische Linie
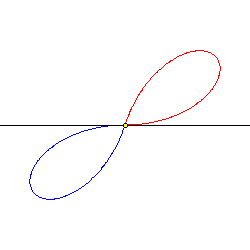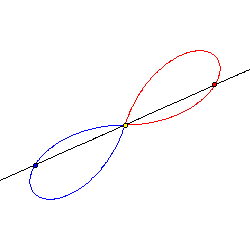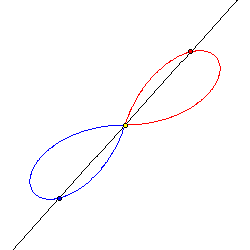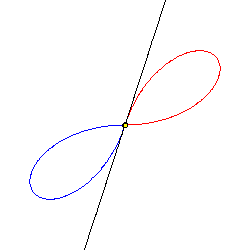
Jeder Punkt der Lemniskate kann vom Mittelpunkt aus gesehen werden.
Zur Zeit t = 0 befinden sich zwei Punkte A (rot) und B (blau) auf einer geodätischen Linie im Punkt M (gelb). Die geodätische Linie rotiert um den Punkt M mit konstanter Winkelgeschwindigkeit. Die beiden Punkte A und B entfernen sich nun stetig von M jeweils in eine Richtung auf der rotierenden geodätischen Linie. Nach einer Zeit t0 bleiben beide Punkte stehen und nähern sich M, umgekehrt wie sie sich entfernt hatten, wieder an. Die Lemniskate ist dann die Bahn beider Punkte A und B.

"unschöne Lemniskaten"
- Um zu verhindern, dass die Lemniskate überzieht, wie im obigen Bild links, ist zu fordern, dass der Wende-Zeitpunkt t0 nicht erreicht wird, nachdem die geodätische Linie sich bereits mehr als 90° gedreht hat.
- Außerhalb der Schleife darf natürlich nichts passieren, d.h. die beiden Punkte A und B müssen nach der doppelten Wendezeit im Mittelpunkt ruhen.
- Damit die Lemniskate keine Knicke bekommt, muss sich die Geschwindigkeit der Punkte A und B stetig ändern. Zur Zeit t0 muss die Geschwindigkeit daher null sein.
- Eichenlaub hat zwar auch seinen Reiz, soll hier aber nicht auftauchen. Deshalb darf die Geschwindigkeit der Punkte A und B zwischen 0 und t0 nur maximal einmal ansteigen.
Anders ausgedrückt:
Es gibt eine in den Intervallen J1 = [0, φe] und J2 = [180°, 180°+φe] zweimal stetig differenzierbare Funktion f, die jedem Winkel φ einen Abstand ε zuordnet, so dass gilt:
f(0) = 0
f(φ) = f(φe-φ)
f(φ) = f(φ+180°)
f(φ) = 0, für φ außerhalb J1 und J2
f'(φ) > 0, für φ Element aus ]0, φe/2[
f'(φe/2) = 0
f'(φ) hat im Intervall [0, φe/2[ maximal ein lokales Maximum.
Mit dieser Definition gibt es nun auch eindeutig bestimmbar Lemniskaten auf gekrümmten Flächen mit einer Metrik.
Die einzelnen Lemniskaten
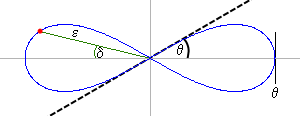
Die Kardan-Lemniskate mit den relevanten Winkeln
Kardan-Lemniskate
In Polarkoordinaten lässt sich die Kardanlemniskate am einfachsten schreiben. Es ist dann:
cos(θ) = cos(ε) ∙ cos(δ)
(Die gleiche Formel ergibt sich auch für das rechtwinklige sphärische Dreieck mit θ als Hypotenuse.)
Der Winkel θ ist der Winkel mit dem die Lemniskate die Abszisse schneidet. Die Winkel ε ist der Polarwinkel und der Winkel δ ist dann der Meridian.
Die Fläche der Kardan-Lemniskate auf der Einheits-Kugeloberfläche ist:
F = 4∙(θ - cos(θ)∙ln(1/cos(θ) + tan(θ)))
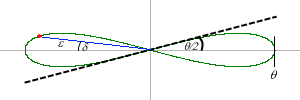
Die Basis-Lemniskate mit den relevanten Winkeln
Basis-Lemniskate
Die Basis-Lemniskate verdankt ihren Namen dem Umstand, dass sie invariant gegenüber Winkelverschiebungen ist. Sie schneidet die Abszisse mit dem Winkel θ/2 und hat folgende Polarkoordinaten-Darstellung:
cos(θ/2) = cos(ε/2) ∙ cos(δ)
Die Fläche der Basis-Lemniskate auf der Einheits-Kugeloberfläche ist:
F = 4∙(θ - sin(θ))
(Die gleiche Formel ergibt sich auch für die x-Koordinate beim Abrollen der Zykloide in Parameterdarstellung.)
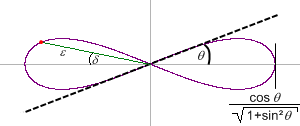
Die Doppel-Lemniskate mit den relevanten Winkeln
Doppel-Lemniskate
Diese ist etwas schwieriger. Die Polarkoordinaten-Darstellung lautet:
cos(θ)/Wurzel(2) = cos(arccot(cos(ε))) ∙ cos(δ)
Zum Glück braucht kein Mensch deren Flächeninhalt.
Nr. 4 bis Nr. 9
Die Polarkoordinaten-Darstellungen der anderen Lemniskaten? Äh, jaja, äh... Ich habe die Frage schon verstanden.
Die Analemma von Vitruv
Ich konnte zeigen, dass die Analemma von Vitruv eine verschobene Basis-Lemniskate ist. Die
Analemma ergibt sich, wenn man ein Jahr lang jeden Tag genau 24 Stunden später ein Foto vom Himmel mit der Sonne macht und dabei die Kamera immer auf den gleichen Punkt auf der Erde richtet (also nicht verstellt).
Die Erd-Analemma am Morgenhimmel
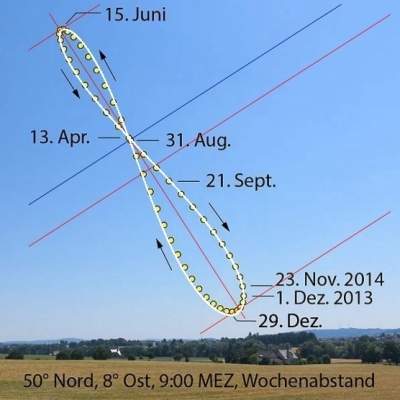
Bild weiterverarbeitet aus der deutschen Wikipedia
Es stellt eine beachtliche Leistung dar, den Unterschied in der Tageslänge mit den damaligen Mitteln (Wasseruhren) herausgefunden zu haben.
Die Berechnung von Vitruv ist allerdings unbrauchbar.
Anwendungen der Lemniskaten
- Na, hauptsächlich für meine Zédolille Windmühle. denn dadurch dass ich schräg nach hinten laufe, laufe ich senkrecht zum scheinbaren Wind und der ist entscheidend. Damit nehme ich dem Winddruck die Spitze und brauche viel weniger Material bei gleicher Leistung.
- Die Umkehrung ist ein neuer Schiffsantrieb mit weniger Kavitation und Energieverlust durch die Verwirbelung des Wassers.
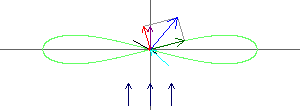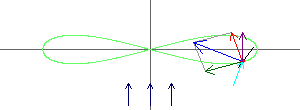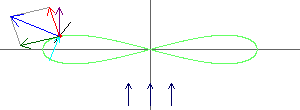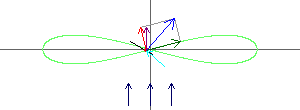
die Lemniskate als Windmühle mit den Vektoren
